oop-shapes.cpp
/* oop-shapes.cpp. Code generated using Microsoft Visual C++.
Using object-oriented programming, this program creates shapes,
displays their properties, and prints them.
The following notes are referred to in the comments of the code below:
Note 1: "public" is used to specify the level of information hiding.
Although this is an important object-oriented feature, each OOPL
implements it differently, so it is beyond the scope of this introduction.
In this program, just ignore the keyword "public".
Note 2: A method in a class with the same name as the class is called
a constructor. It is automatically run when the object is created, so
we don't need a separate create() method for each class.
Note 3: Note that these constructors have the same name. This is
called polymorphism. The compiler figures out the correct one to run
by matching the argument lists.
Note 4: Although using a create method is generally poor OOP practice,
I'm using it here because the code to circumvent it would be too
complicated for those unfamiliar with C++. Note, though, that objects
themselves call create; the program doesn't expect programmers to do this
in main. Thus the create() method is semi-automatic.
*/
#include <iostream>
#include <math.h>
using namespace std;
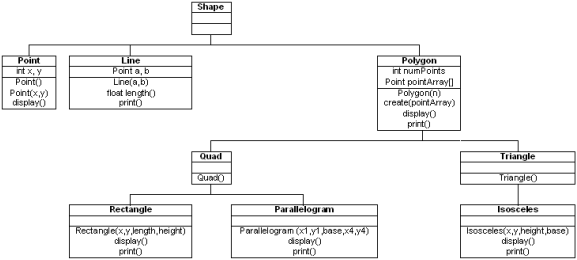
/* Shape
This is the root class for our hierarchy. Even though it doesn't do
anything here, it's still important because if we want to add
functionality later, it's here for us.
*/
class Shape {
};
/* Point
Point represents an x-y coordinate that can display itself.
*/
class Point: public Shape {
public: // See note 1
int x, y;
Point() { // See notes 2 and 3
x = 0;
y = 0;
}
Point( int x_coord, int y_coord ) { // See notes 2 and 3
x = x_coord;
y = y_coord;
}
void display() {
cout << "(" << x << "," << y << ")";
}
};
/* Line
Line represents two connected Points. It can return its length, and print
itself.
*/
class Line: public Shape {
public:
Point a, b;
Line( Point first, Point second ) {
a = first;
b = second;
}
float length() {
return sqrt( pow(a.y-b.y, 2) + pow(a.x-b.x, 2) ); // Pythagoran formula
}
void print() {
cout << "Line from ";
a.display();
cout << " to ";
b.display();
cout << "n";
}
};
/* Polygon
Polygon represents a closed 2-D shape. It needs its sub-classes to create it
(see note 4), but other than that Polygon can display and print itself. Note
that it can do this without even knowing how many points or sides it has.
*/
class Polygon: public Shape {
public:
int numPoints; // The number of points == number of sides
Point* pointArray; // Contains each subsequent point in the Polygon
Polygon( int n ) {
numPoints = n;
}
void create( Point pointList[] ) { // See note 4
pointArray = new Point[numPoints];
for ( int i=0; i<numPoints; i++ )
// assign the pointArray the first n Points in corners array
pointArray[i] = pointList[i];
}
void display() {
pointArray[0].display(); // display the anchor point
cout << "n";
for ( int i=0; i<numPoints-1; i++ ) {
// display all but the last line information
cout << "Line " << i+1 << "-" << i+2 << " is ";
Line l( pointArray[i], pointArray[i+1] );
cout << l.length() << " points long.n";
}
// display the last line information
cout << "Line " << numPoints << "-1 is ";
Line l( pointArray[numPoints-1], pointArray[0] );
cout << l.length() << " points long.n";
}
void print() {
for ( int i=0; i<numPoints-1; i++ ) {
// print all but the last line
Line l( pointArray[i], pointArray[i+1] );
l.print();
}
// print the last line
Line l( pointArray[numPoints-1], pointArray[0] );
l.print();
}
};
/* Quad
This simple class looks rather barren. Yet the one thing it does is vital:
it creates itself as a 4-sided Polygon.
*/
class Quad: public Polygon {
public:
Quad(): Polygon( 4 ) {}
};
/* Rectangle
Finally we get around to what we've been trying to do: create a Rectangle!
By the end of this class definition, we've written 91 lines of code--over
three times as many as using the traditional structured programming style!
Not only did it take longer to code, but the design process of creating six
classes just to create one Rectangle object is much more time-consuming.
That doesn't seem to be much of an argument for OOP, but it does bring up a
major feature of OOP: object-oriented design can be quite intensive.
Actually, 90% of the work in OOP is in the design process. But once you've
invested the time in doing all that design work, you start reaping the
benefits pretty rapidly. When we create our next class, Triangle, we'll see
this.
Notice that Rectangle's methods are pretty simple: it does nothing but
identify itself as a Rectangle, as opposed to any other kind of Quad.
It's constructor (see note 2) defines a Rectangle, and its display()
and print() methods simply label the printout as a Rectangle.
*/
class Rectangle: public Quad {
public:
Rectangle( int x, int y, int length, int height ) {
Point corners[] = { Point(x,y),
Point(x+length,y),
Point(x+length,y-height),
Point(x,y-height),
};
Quad::create( corners );
}
void display() {
cout << "Rectangle Properties: Top-left corner is ";
Quad::display(); // display whatever Quads usually display
/* Note that what actually runs is the
display() method in Polygon.
*/
}
void print() {
cout << "Rectangle:n";
Quad::print(); // print whatever Quads usually print
}
};
/* Triangle
This is the first part of Task 2. Similar to Quad, all this class does is
create itself as a 3-sided Polygon.
*/
class Triangle: public Polygon {
public:
Triangle(): Polygon( 3 ) {}
};
/* Isosceles
Now we begin to see the benefits of OOP. Triangle and Isosceles together
take 24 lines of code (compare 27 in the traditional implementation
of Isosceles), which seems minimal, except that the changes in our cut-
and-paste here are very minor: just the Isosceles definition in the
constructor (see note 2) and the labels in display() and print().
*/
class Isosceles: public Triangle {
public:
Isosceles( int x, int y, int height, int base ) {
if ( base%2 == 1 )
// base is odd, so increment to allow even division by two
base++;
Point corners[] = { Point( x, y ),
Point( x+(base/2), y-height ),
Point( x-(base/2), y-height ),
};
Triangle::create( corners );
}
void display() {
cout << "Isosceles Properties: Topmost point is ";
Triangle::display();
}
void print() {
cout << "Isosceles:n";
Triangle::print();
}
};
/* Isosceles
Adding Parallelogram took only 19 lines of code, with only half of those
even requiring minor modifications. The true power of OOP becomes
apparent when building large, complex systems. It helps minimize bugs in
the development process and makes it easy to add new functionality.
*/
class Parallelogram: public Quad {
public:
Parallelogram( int x1, int y1, int base, int x4, int y4 ) {
Point corners[] = { Point(x1,y1),
Point(x1+base,y1),
Point(x4+base,y4),
Point(x4,y4),
};
Quad::create( corners );
}
void display() {
cout << "Parallelogram Properties: Top-left corner is ";
Quad::display();
}
void print() {
cout << "Parallelogram:n";
Quad::print();
}
};
int main() {
Rectangle r( 3,10, 6, 8 ); // anchor point, length, height
cout << "n";
r.display();
cout << "n";
r.print();
Isosceles i( 3,10, 6, 8 ); // anchor point, height, base
cout << "n";
i.display();
cout << "n";
i.print();
Parallelogram p( 3,10, 6, 5,7 ); // upper anchor, base, lower anchor
cout << "n";
p.display();
cout << "n";
p.print();
return 0;
}


